アプリケーション開発の最前線から 第7回 フェーズフィールド法の開発者・高木さんに聞く
あえて境界をぼやかすことでいいものが生まれることがある。例えば、京都の祇園祭に出向けば、山鉾の飾りには西洋や中東からの舶来品が使われており、和洋の境界にこだわらない姿勢がきらびやかな京文化を完成させていることに気付く。1と0 に冷徹に支配される計算科学の世界にも、境界をぼやかすことで計算がうまくいくという手法がある。そんな手法である「フェーズフィールド法(PF法)」と、その研究に取り組む京都工芸繊維大学の高木知弘さんを紹介する。
話し手: 高木知弘 京都工芸繊維大学工芸科学研究科 准教授
聞き手: 米澤進吾 京都大学理学研究科 助教
界面をぼやかす計算手法
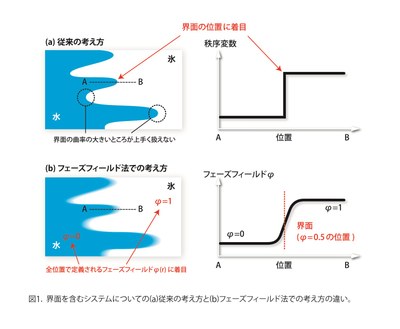 この変数φは界面の両側の相を定義する「場」のようなものなので、「フェーズフィールド(Phase-Field:PF)」と呼ばれる。あとはφと他の諸量の関係を表す方程式やこれらの時間変化を記述する方程式を連立して計算すれば、界面の変化を計算することが可能になる。しかも、このモデルでは界面の曲率エネルギーが自然に取り入れられている。つまり、従来の方法では難しかった複雑な形状の界面の正確なシミュレーションが可能になるのである。このようにPFを導入して、界面を含むシステムを扱う方法を「フェーズフィールド法(PF法)」と呼ぶ。
この変数φは界面の両側の相を定義する「場」のようなものなので、「フェーズフィールド(Phase-Field:PF)」と呼ばれる。あとはφと他の諸量の関係を表す方程式やこれらの時間変化を記述する方程式を連立して計算すれば、界面の変化を計算することが可能になる。しかも、このモデルでは界面の曲率エネルギーが自然に取り入れられている。つまり、従来の方法では難しかった複雑な形状の界面の正確なシミュレーションが可能になるのである。このようにPFを導入して、界面を含むシステムを扱う方法を「フェーズフィールド法(PF法)」と呼ぶ。高木さんとPF法の出会い
高木さんは、PF法と出会う以前は機械部品の実験およびシミュレーションの研究をしていた。主に用いていたシミュレーション手法は、物体を細かい領域に分割して計算を行う有限要素法であった。しかし2000年ごろになると、徐々に汎用の有限要素法ソフトが出回り始め、企業も積極的に有限要素法に取り組むようになった。そのような状況の中、高木さんは「企業でもできるような研究を大学でやっていていいのか」という思いを持つようになった。そんな中、恩師の冨田佳宏さんに提示されたテーマの中にPF法が含まれていた。当時の高木さんの研究対象であったマクロな物体の機械的な性質は、より微視的な結晶組織によって強く支配されている。例えば、日本刀を考えてみよう。刀鍛冶は鉄を熱して叩くことで元の原料よりもはるかに強靭な刀身を作り上げるが、ここには結晶組織構造の変化が大きくかかわっている。高木さんは、結晶組織の作られ方にまで踏み込めるPF法に魅力と将来性を感じて研究対象として取り組むようになった。
高木知弘たかき ともひろ 京都工芸繊維大学 准教授機械分野だけでなくさまざまな分野にフェーズフィールド法を広めるべく研究している。フェーズフィールズ法に関して2011年ゴートン・ベル賞特別賞をはじめとして、APACM Award for Yong Investigators in Computational Mechanics、日本機械学会の講演賞・論文賞・業績賞など多数の受賞歴がある。 |  |
|---|
高木さんがPF法の研究を始めてすぐに、この方法の強みが理解できた。まず、さまざまな方法との親和性が高いのがPF法の特徴である。例えば、熱拡散方程式と組み合わせれば潜熱を発生する凝固のような現象が記述できるし、流体の方程式と組み合わせて対流のある場合の界面の移動も記述できる。また、機械分野との相性も予想通り非常に高いことが分かった。高木さんの所属する機械分野の学会でも、当初はほんの数名がPF法の発表をするにすぎなかったが、すぐにこの方法は受け入れられ広まった。「流行にうまく乗ることが出来た面もある」と当時のことを謙虚に振り返る高木さんだが、むしろその流行を作った中心が高木さんだったといえよう。
2007年に京都工芸繊維大学に移った後も、PF法を軸として研究を進めている。PF法を、自分の研究分野に応用する手段として研究する研究者は多い。一方高木さんは「PF法を軸としてできることをなんでもやってみたい」と語る。PF法を研究の出発点としている意味では日本で唯一の「PF法の専門家」といっていいかもしれない。現在では、結晶組織の成長・変化の問題だけでなく、神経細胞の成長モデル、材料内の亀裂発展のシミュレーション、または力を支える構造形状の最適化など、幅広い分野の研究を手がけている。
スパコンが拓くさらなる実力
PF法の一つの問題点は、計算時間の問題である。複雑な界面構造を記述しようとするとそれだけ計算に用いるメッシュを細かくしなければならず、計算量が大きくなってしまうのである。特に、シミュレーションを現実に役立てようとすると三次元の計算が必要になるが、三次元計算に必要なメッシュの数は二次元の場合よりも数ケタも大きく、通常の計算機では手に負えない。そこで、スパコンが威力を発揮する。
スパコンとPF法の相性の良さをまざまざと見せつけたのが、「スパコン界のノーベル賞」とも呼ばれるゴードン・ベル賞受賞(2011年)であろう。高木さんらのグループによる、東工大のスパコンTSUBAME2.0を用いた合金の樹枝状結晶成長の数千×数千×数千メッシュもの三次元シミュレーションが受賞対象だ。実はPF法は1メッシュあたりの計算量が比較的大きいため、スパコンの実力を発揮しやすいという特徴をもともと持っているのである。そこに、メモリアクセス方法などに多くの改良を施すことによって、2ペタフロップスという非常に高い実行性能を達成した。高木さんは、受賞によって明らかに「PF法が分野外の人の目につくことが多くなった」という。この受賞がPF法の一つのターニングポイントに後世位置づけられるのは間違いない。
さらにスパコンの実力を発揮すると期待されるのが、マルチスケール計算である。まず、マクロスケールの試料を有限要素法で分割し、それぞれの変形や内部応力などを計算する。通常はここで終わりなのだが、高木さんはそれぞれの要素の中で生じる結晶組織の変化をPF法で計算できるようにしたのだ。この組織変化によって各要素の機械的性質が変わるため、それを反映して再び有限要素法とPF法を繰り返すのである。このようにすれば、例えば「強く変形した部分は固くなる」というような現実的な現象をミクロレベルで取り込みながらマクロスケールの変形をシミュレートするということが可能になる。こういったマルチスケール計算は、非常に時間がかかるために小さい領域しか扱えなかったが、スパコンを用いれば現実的な大きさの材料のマルチスケール計算も可能になるであろう。
PF法の未来
今後、PF法はどのように発展していくのだろうか。高木さんは、第一に、対流の効果をより正確に取り上げた上での凝固シミュレーションが重要ではないかと考えている。物質が凝固する際には液体側に必ず対流が生じているはずで、それを取り入れなければ再現できない現象も多いはずである。また、第一原理計算のような原子スケールの計算とPF法をつなぐ方法論の構築も必要であるという。これらが実を結べば、材料を作るうえでのあらゆるプロセスをシミュレーションできるようになり、材料研究に革新を起こせるであろう。第二に、理論と実験をより詳細に比較する地道な取り組みを進めていくことも大切であると高木さんは考えている。
高木さんはPF法の普及にも努めている。PF法に関する話題を集約したホームページ(http://www.pfm.kit.ac.jp/)を立ち上げたり、初学者向けの著作を出版したり、講習会を開催したりと、幅広い活動をおこなっている。一方、独立のアプリケーションとして整備するという取り組みはまだ途上である。PF法は単独ではあまり意味を持たず、他の方程式と組み合わせることで意味のあるシミュレーションができる。そのような特性があるため、「何にでも使える一般的なPF法アプリケーション」というのは開発が難しそうである。まずは、ライブラリのように、他のプログラムに組み込むツールとして公開することで、より多くの人がPF法を使えるようにするための第一歩を踏み出していく。
高木さんとPF法が起こすさらなるイノベーションはすぐそこに迫っている。
◆インタビュー後記◆米澤進吾よねさわしんご 取材は8月の暑い日に行われたのですが、面白いシミュレーション結果を幾つも見せて頂いて、驚きの連続でした。特にマルチスケールのシミュレーションは「こんなことまでできるのか!」と感銘しました。実はフェーズフィールド法の基本式と、私の研究している超伝導状態を記述する理論式はほとんど同じ形式をしており、親近感を感じた取材でもありました。 |  |
|---|