Interview with Masato Kobayashi, developer of DC
Masato KobayashiAssistant Professor, |
Interviewer: Yu YachiPh.D. Candidate, Division of General Culture, |
 “Divide each difficulty into as many parts as is feasible and necessary to resolve it,” said the philosopher Rene Descartes. Since ancient times, the idea of “divide and conquer” has been widely used in the realm of politics, etc. But in recent years it has also been applied to methods of calculation for large-scale systems ̶ in particular, as a method of speeding up electronic structure calculations.
“Divide each difficulty into as many parts as is feasible and necessary to resolve it,” said the philosopher Rene Descartes. Since ancient times, the idea of “divide and conquer” has been widely used in the realm of politics, etc. But in recent years it has also been applied to methods of calculation for large-scale systems ̶ in particular, as a method of speeding up electronic structure calculations.
Masato Kobayashi, who has studied the divide-and-conquer method, is working to incorporate electron correlations in order to further increase the accuracy of this method. He has succeeded in developing DC, new application software based on his original idea.
Computers and quantum chemical calculations
“Everyone is fascinated when they do a laboratory experiment and see the blue color of copper ions appear. But why is the color blue? That’s something very difficult to figure out. These kinds of fundamental questions can be understood through quantum chemistry. That’s why I was attracted to it.” So says Dr. Masato Kobayashi in explaining why he chose the path of quantum chemistry. The behavior of electrons and atomic nuclei determines the structure and properties of all matter. Quantum chemistry provides theoretical explanations for this behavior. Electronic structure ̶ electron density, energy state, spin state and so on ̶ can be calculated by solving the Schrödinger equation. In practice, it is not possible to exactly solve equations for many-body systems made up of numerous electrons and atomic nuclei. For this reason, approximation is used for calculation.
Nevertheless, even when a computer with high-level computational ability like the K Computer is used, it takes an enormous amount of time to execute calculations with highly accurate approximation, those capable of adequately recreating the properties of matter. If the number of atoms is N, computing time increases proportionally to N⁵-⁷. Suppose a computer takes one second to perform calculations for a single atom. That computer would need from 30 seconds to two minutes to perform calculations for two atoms. If there are 100 atoms, the computer would need anywhere from 300 years to three million years.
Hardware advancements alone will not be sufficient to decrease this enormous computing time. The real key will be to develop software that uses a completely new theory for approximation calculations and can take advantage of the latest hardware. That key is now in place, in the form of the divideand-conquer method and the DC application software based on this method.
“Divide difficulty into parts”
The “divide-and-conquer” method takes the approach of dividing a problem that cannot be calculated as is into smaller partial systems and then solving those small problems. In quantum chemistry, the divide-andconquer method divides large molecules up, performs calculations for each part, and then adds up the results.
Although the concept is simple, in practice a variety of measures are needed. First, the target molecule must be divided up into several non-overlapping subsystems. This means that the impact of the surrounding domains will not be included in the calculations, resulting in low accuracy. For this reason, the subsystems with the peripheral atoms added as buffer domains are calculated separately (Fig.1). Then, the results of all subsystems are accumulated with excluding contributions from the buffer domains. The process is repeated until the electron density derived in this manner converges to a certain value at every point in the space. With the divide-and-conquer method, calculations are performed with the entire system divided up into subsystems of a uniform size, so the calculation time is directly proportional to N. Using the previous example, calculations for 100 atoms could be performed in 100 seconds. Moreover, as the calculations for each subsystem are performed independently, they can be done efficiently using parallel computing with modern supercomputers like the K Computer that are made up of numerous processing nodes. One of the features of the divide-and-conquer method is that even if the subsystems are made smaller, for example divided up into individual atoms, the accuracy is not greatly reduced. Dr. Kobayashi focused on this attribute and wanted to create a program that would be easy for anyone to use.
Encounter with Energy Density Analysis
To achieve higher calculation accuracy, the effect of electron correlation must be incorporated. With the conventional divide-andconquer method, the interaction between electrons is averaged. The difference between this averaged interaction and the exact interaction is referred to as “correlation energy.”
However, there was a major problem with applying the divide-and-conquer method to calculations that incorporate electron correlation. The values derived with the conventional divide-and-conquer method were those for the correlation energy for each subsystem including the buffer domains, and simply adding these up will result in duplicate calculation. It was essential that this problem be resolved.
One day, Dr. Kobayashi heard a presentation on Energy Density Analysis (EDA) at a laboratory seminar. That gave him the idea to incorporate EDA into the divide-andconquer method.
Energy Density Analysis is an analysis technique in which the energy of the entire molecule is allocated to individual atoms. Dr. Kobayashi thought that EDA might make it possible to derive the correlation energy for individual domains without including the buffer domains. Adding these together would enable even the correlation energy to be determined in a calculation time that was proportional to N. This became the EDA divide-and-conquer method developed by Dr. Kobayashi.
“In physics, it might be taboo to apply an analysis method like EDA to calculation theory,” says Dr. Kobayashi. “For that reason, I was very uneasy as to whether it would actually work. But I tried several different methods, and the method that uses EDA gave the most accurate results, and the calculation time was also short.”
Calculating larger systems with higher accuracy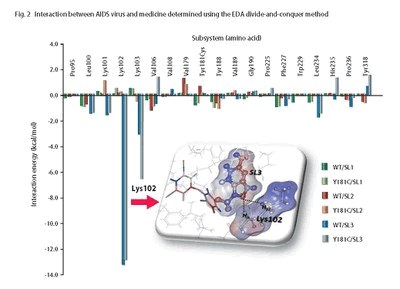 Combining Energy Density Analysis with the divide-and-conquer method made it possible to quickly perform highly accurate calculations that include electron correlation. This method is well-suited to the investigation of substances in which electrons are not localized and move from place to place. With the K Computer, it is even possible to perform ultra-high accuracy calculations for nanosize materials. For example, the power generation efficiency of organic solar cells is greatly affected by the electrical properties of charge transport materials like pentacene. Using the divide-and-conquer method to calculate the charge mobility is making it possible to design solar cell materials that have greater efficiency.
Combining Energy Density Analysis with the divide-and-conquer method made it possible to quickly perform highly accurate calculations that include electron correlation. This method is well-suited to the investigation of substances in which electrons are not localized and move from place to place. With the K Computer, it is even possible to perform ultra-high accuracy calculations for nanosize materials. For example, the power generation efficiency of organic solar cells is greatly affected by the electrical properties of charge transport materials like pentacene. Using the divide-and-conquer method to calculate the charge mobility is making it possible to design solar cell materials that have greater efficiency.
Moreover, Energy Density Analysis makes it possible to calculate the correlation energy for each domain, enabling direct analysis to determine, for example, locations where interaction is strong, or locations that are unstable and where the bond is about to break. For example, it is possible to conduct a detailed investigation of the bond between the HIV (AIDS virus) and the reverse transcriptase inhibitor that is designed to inhibit the virus (Fig. 2). In the future, this type of information will not only make it possible to safely pursue the development of more effective drugs and enable the costs to be greatly reduced, it may even make it possible to predict side effects.
At present, DC, the EDA divide-and-conquer application software, is available to the general public as freeware. It is incorporated into GAMESS, the world’s most commonly used freeware for quantum chemical calculations, as an option. Dr. Kobayashi had customized GAMESS so he and his colleagues could use his own method within the program. In order to make his software available to as many people as possible, he contacted Iowa State University, which manages GAMESS, and got the program formally adopted.
More recently, Dr. Kobayashi has just started adapting the program for the K Computer. The K Computer is made up of 640,000 cores. “It’s completely unlike any supercomputer up to now, so the software requires special tuning,” he says. “I still have several hurdles to overcome. It’ s a challenge for the future.” I was struck by the obvious joy in his voice.
|
|

 Masato Kobayashi
Masato Kobayashi Yu Yachi
Yu Yachi