RSDFTの開発者・岩田さんに聞く
|
話し手:
|
 |
「第一原理計算とは?」
私たちの身の回りにあるさまざまな物質。その色や固さといった性質もさまざまだが、これらの性質はどのように決まっているのだろうか? 物性物理学は、物質の性質(物性)を知るために、電子や原子核というミクロなレベルでそれらのふるまいを調べる学問だ。しかし、ミクロのレベルでは、実験だけからすべてのふるまいを理解するのは困難で、計算や数値実験が重要な役割を果たしている。
その重要な計算手法のひとつが第一原理計算だ。「第一原理」とは「他の原理や仮定などから推論することのできない最も基本的な原理」を意味する言葉で、物理学だけではなく哲学などでも使われる。研究分野が異なると「第一原理」の意味するところが微妙に違ってくることを、岩田さんは丁寧に説明してくれた。 「物性物理学での第一原理とは、量子力学の基本法則のことを指します。そこから出発して、電子の質量や電荷といった基本物理量以外には、実験結果と合わせるための調整パラメータの導入をいっさい行わないで計算することを“第一原理計算”と呼んでいます。
量子力学の第一原理に基づいて、この世に存在し得るすべての物質の性質を予測することが物性物理学の究極の目標です。しかし、第一原理から出発してすべての計算を近似なしで行うことは、実際上は不可能です。扱う系の大きさや研究対象によって、計算に用いる基本方程式を変えたり、近似を用いて計算方法を改良したりしなければいけないのです」「第一原理計算」と一般的に呼ばれているものでも、基本となる方程式や近似の度合いによってさまざまな第一原理計算が存在する。その中で、岩田さんが開発を進めてきた実空間密度汎関数法(Real-SpaceDensity-Functional-Theory、以下RSDFT)は、1998年にノーベル化学賞を受賞した「密度汎関数理論」に基づいて、多電子-多原子核系の量子力学的第一原理計算を行うソフトウェアだ。第一原理計算は、「経験的パラメータを入れた手法」に比べると、信頼性の高い物性予測が可能となるが、扱える原子数が少なくなってしまうというデメリットがあり、せいぜい数百~1000原子が限界だろうと言われてきた。それに対して、「RSDFTを使うと、これまでの3桁も大きい10万原子の計算ができるようになります」という。
|
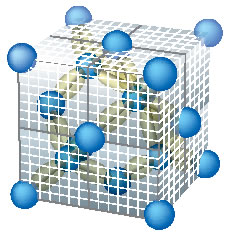
図1. 実空間計算のための離散化と並列化 シリコン結晶のユニットセル | |
|---|---|
|
|
|
| 空間中に配置されたシリコンの原子核(青色)の周りに、連 続的に分布する電子(黄色)が存在する。実空間法では、こ の連続的な電子密度分布を離散的なメッシュ点上で表す。 |
現実の空間のメッシュは、大きなブロックに分けられ る。それぞれのブロックは異なるCPUが担当し、隣り同 士でたがいに通信しながら協調して計算を実行する。 |
「RSDFTとはどんなソフト?」
物性を明らかにするには、電子状態を計算することが非常に重要だ。われわれの身の回りの物質を考える場合、通常、価電子(外殻電子)とイオン(内殻電子と原子核の集合体)で構成される系を考えれば十分である。そうした上で、RSDFTでは、電子状態の計算を、密度汎関数理論を用いて行っている。密度汎関数理論は、電子の密度分布のみから電子のエネルギー基底状態(波動関数で表される)を計算できるという理論で、シュレーディンガー方程式を解くよりも計算が簡単になるので、多電子系を解くのに適している。「 密度汎関数理論の基本方程式(コーン・シャム方程式)を、計算機上でいかに効率よく計算させるかを工夫したソフトウェアがRSDFTなのです」と岩田さん。RSDFTでは、偏微分方程式の形をしたコーン・シャム方程式を差分方程式の形で表し計算を行っているのが特徴だ。これまで行われてきた数百原子までの第一原理計算では、波動関数を単純な平面波の重ね合わせで表現し、高速フーリエ変換(FFT)を用いる計算手法が大きな成功を収めてきた。しかし、計算機が大型化し、超並列化に向かっている中で、FFTは通信に膨大な時間がかかるため大規模並列計算のボトルネックになっていた。そこで、RSDFTでは、並列計算機の性能を十分に引き出せると理論的に知られていた実空間法を用いて波動関数を計算する手法を開発してきた。実空間法とは、空間を離散的な3次元のメッシュで表し、そのメッシュ点上での波動関数の値を数値計算で直接求めていく手法だ。そして、メッシュで区切られた空間をいくつかのブロックに分け、それぞれのブロックをそれぞれのCPUに対応させて計算している。つまり、分割された現実の空間が、計算機上でもCPUの単位として同じように分割されているのだ(図1)。そうすることによって効率よく仕事を割り振り、無駄の少ない並列計算ができるようになった。実空間法で波動関数を計算するということは、FFTを用いる必要がなく、よって通信の問題を解消できたことになる。
|
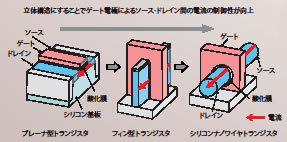
図2. 微細化に伴うトランジスタの構造変化 立体構造にすることでゲート電極によるソース-ドレイン間の電流の制御性が向上 | 図3. 断面の直径5ナノメートルの シリコンナノワイヤの原子モデル |
|---|---|
 |
 |
「計算機科学者との交流が飛躍に!」
RSDFTには、計算効率の向上に関してもう一つのウリがある。グラム・シュミットの直交化のアルゴリズムだ。波動関数の直交化は必要不可欠な計算だが、その計算量がメッシュ点の数の3乗に比例するため、シミュレーションする物理系が大きくなると、計算時間が爆発的に増えるという問題があった。「ベクトルの内積計算を基本とするアルゴリズムから、コンピュータで処理しやすい行列積計算を基本とするアルゴリズムに置き換えることで、解決しました」。計算機科学の知恵を借りることによって、計算効率を飛躍的に向上することが可能となった。
RSDFTの開発は、筑波大学で開発されてきたPACS-CS(計算科学向け超並列クラスタ)プロジェクトから続いている。月1回の計算機科学との合同ミーティングで、岩田さんはRSDFTで何をやりたいかを計算機科学の研究者に説明した。「何度も説明していくうちに、いろいろとアドバイスをもらえるようになりました。最初は専門用語がよくわからなかったのですが、月に1回のペースで顔をあわせて直接コミュニケーションをとっていたら、いつのころからかすんなり話が通じるようになってきたんです。グラム・シュミット以外にも、分野外である計算機科学の最新理論を知ることができたことも、アルゴリズムの構築にとても役に立ちました」と、当時を振り返る。計算機科学の研究者との密なコミュニケーションが成功の秘訣だったようだ。
一方で、岩田さんにとってRSDFTの開発に集中していた1~2年は、フラストレーションがたまる時期でもあった。岩田さんの本分は物理学の研究だ。ソフトウェア開発に多くの時間を取られていたため、データを出し、その成果を論文として公表するという研究者としてやるべき仕事ができなかった。このままで大丈夫なのかという不安と戦いながらRSDFTの開発に取り組んでいた。モチベーションをどうやって保っていたのか?「 できあがった暁には、何でも計算できるようになるんだ。インパクトが大きいはずだと信じてやっていましたね。気が長いほうなので…」。岩田さんは持ち前のねばり強さで成果が出せない期間を乗り越えたが、日本では、ソフトウェアの開発だけでは業績としての評価につながりにくいのが現状だ。「今後は、こうした状況を改善していきたいです」と、CMSIの一員としての自覚を見せてくれた。
「次世代半導体デバイスへの応用」
「京」を使えば数万~10万原子規模の第一原理計算を実行できるようになる。では、どんなことに応用できるのだろうか ? 10万原子のシミュレーションとして岩田さんたちがターゲットにしているのは、半導体デバイスだ。半導体デバイスは、私たちの身の回りにあるパソコンや携帯電話などの電子機器に不可欠であり、消費電力を抑えるため、また高速化を実現するため、デバイスの小型化が進んできた。数ナノメートルまで小さくなったデバイスでは、電子の量子力学的ふるまいが直接性能に影響を与えるようになる。実験のみでは詳細なデバイス設計方針を立てることが難しく、第一原理計算への期待が高まっている。半導体デバイスに使われてきた電界効果トランジスタは平らなシリコン基板の上に酸化膜とゲートと呼ばれる金属が乗った構造になっている。ゲート電極の電圧をオン・オフさせてシリコンに電流を流すか流さないかをコントロールし、スイッチとして機能させている。ところが、あまりにもサイズが小さくなりすぎて(数ナノメートル)、電流オフの状態でもごわずかな電流が漏れるようになり、小型化には限界が近づいている。そこで、これまでの二次元積層構造ではなく、円柱や角柱の形をしたナノワイヤ型トランジスタが次世代半導体デバイスとして提案されている。ナノワイヤ型トランジスタは、酸化膜とゲート金属がシリコンでできたワイヤ(シリコンナノワイヤ)を包み込むような構造をしている(図2)。実際のシリコンナノワイヤ型トランジスタでは、断面の直径が10~20ナノメートル、電流の流れる距離が5~10ナノメートル程度になると予想されている(図3)。その中にはおよそ10万個のシリコン原子が入っており、ちょうど「京」を使って計算できるサイズと同じくらいになる。「“京”を使った計算で、ナノワイヤ型トランジスタの物性を明らかにし、実用化につなげたいと思っています」と、岩田さんは意気込みを語る。
半導体以外では、生体分子への応用に注目している研究者もいる。単純なタンパク質なら、RSDFTを使うことで、分子丸ごとをシミュレーションすることが可能になるのだ。RSDFTは、固体だけではなく液体や気体にも適用できるため、いろいろな物質への応用が期待される。
取材協力:京極真也(東京大学大学院工学系研究科)
図版提供:角嶋邦之(東京工業大学)
【ソフトウェア世界一を目指して】
今年6月、喜ばしいニュースが届いた。第26回国際スーパーコンピューティング会議(ISC'11、p.15参照)でのコンピュータの処理性能を競うTOP500ランキングにおいて、「京」は世界最高性能8.162ペタフロップスで世界第1位を獲得したのだ。この11月には、ソフトウェア開発における世界最高賞「ゴードン・ベル賞」の発表がある。ゴードン・ベル賞はスーパーコンピュータ界のノーベル賞とまで称され、並列計算におけるその年のブレークスルーに与えられる賞だ。RSDFTはこの賞にノミネートし、ファイナリストにも残っている。ソフトウェアでも「世界一」への期待が高まる。
 |
岩田 潤一 いわた じゅんいち 学部時代には電気回路などの計算法を学んだが、計算法の裏付けを独学で勉強しているうちに物理、特に量子力学に興味をもつようになった。大学院では原子核理論の研究室に進み、時間依存密度汎関数法を用いた電子系の光応答の研究で博士号取得。並列計算を始めたのは2005年頃から。2011年8月から、CMSI特任講師として計算科学教育にも携わる。趣味はラーメン、マージャン、ジャンプなど。 |
 |
久保田 好美 くぼた よしみ ◆ インタビュー後記 |