詳細つりあいを満たさないマルコフ連鎖モンテカルロ法

われわれが興味をもっている相転移現象や量子的相関の強い状態の発現は、いまだに理解されていない新奇な物理を豊富に含んでおり、新しい物質設計などへの応用も期待されています。これらの多くの物理現象では多粒子(多自由度) であることが本質で、粒子間の平均量だけに注目する大ざっぱな近似は有効ではありません。人間の手計算で解くことが難しいこれらの問題も、コンピュータをうまく利用することで初めて解析可能となるのです。しかし、むやみやたらに計算機を大規模に使えば済むという問題ではなく、いかにそれらを賢く効率良く使うかが重要です。われわれの取り組んでいるマルコフ連鎖モンテカルロ法にも、それは当てはまります。この手法は多重積分をコンピュータで求める汎用性の高い手法で、物理に限らず、化学、生物、医学、統計、経済など、さまざまな分野で必要不可欠となっています。これまでのマルコフ連鎖モンテカルロ法は、ほとんどの場合、「詳細つりあい」という条件を用いており、半世紀以上の間この条件の枠の中で発展を続けてきました。ところが、この条件は計算の都合上便宜的に用いてきたもので、本来必要な条件ではありません。そこで、われわれはこれまでの常識を破り、「詳細つりあいを満たさずとも正しい計算を可能とする」新しいアルゴリズムを考案しました。このアルゴリズムは、「重みの埋め立て」という幾何学的な手続きにより、効率低下の要因である平均棄却率をいつでも最小化し、多くの場合でゼロにします(図)。計算効率は大幅に改善され、これまでの計算機の数倍から百倍以上の効率を示すことができました。また量子力学的な問題であるスピン系に応用し、スピンの液体状態から固体状態への新しい相転移を見いだしました。この手法はさまざまな分野で用いられているほぼすべてのマルコフ連鎖モンテカルロ法に応用可能であり、今後それらの分野で広く貢献していくと期待されています。

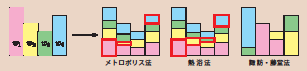新しい手法と既存の手法での「重みの埋め立て」の比較。われわれの手法ではこの場合、棄却率がゼロになる。