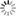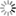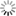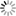Development of multiscale structural design and assessment techniques to improve the performance of metallic structural materials
Interviewee:
|
Interviewer:
|
| Prime Senior Researcher, Research Institute for Ubiquitous Energy Devices, National Institute of Advanced Industrial Science and Technology (AIST) |
CMSI Materials Science |
Objectives of research for this Priority Research Topic
The objective of research in this area is to gain an understanding of the mechanical properties of iron and steel and other metallic
structural materials from the atomic and electron level on up. The strength of a metal is determined by its ease of mobility of dislocations (linear defects). For this reason, metallic materials are not monocrystalline but polycrystalline (aggregates of crystal grains), forming a microstructure in which compounds have been deposited. Microstructures achieve high strength by preventing dislocation mobility by means of their grain boundary (interface between crystal grains), deposits, solute atoms, defect clusters and so on.
First-principles calculations are possible for simple defects and interfaces of such metals. Due to lattice misfit, however, the non-coherent (partially coherent) interfaces between deposits and metals require extremely large supercells consisting of several thousand to several tens of thousands of atoms, making it difficult to perform first-principles calculations. In this Priority Research Topic, the K computer and a cutting-edge calculation method are being used to achieve large-scale first-principles calculations for the interfaces between different phases, grain boundaries, dislocations and so on. The aim is to gain an understanding of the detailed interatomic bonds and energy in microstructures, as well as the dynamic behavior and the effect of
alloy content and additive elements.
Calculation method
OpenMX, a large-scale first-principles calculation code, is being used in this area. OpenMX calculates electron structures using localized atomic orbital basis sets based on density functional theory. A density matrix is determined for clusters within a set range for each atom, and self-consistent calculations are performed to determine electron structure, total energy and the force acting on the atom. The electron structure is determined in a localized manner, making it possible to use order-N calculations, in which the total calculation time is directly proportional to the number of atoms. Use of the K computer is expected to enable large-scale parallelization, and optimization is underway.
QMAS, a plane wave basis set PAW method code, will also be used. Although it cannot handle large systems, QMAS can be used to calculate local stress and local energy, and it is capable of determining the stress and energy distribution at interfaces and grain boundaries and in the area of dislocations with a high degree of accuracy.
First-principles calculations for interfaces between different phases
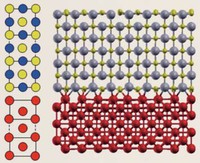
We have begun with calculations for the titanium carbide (TiC) / iron interface. In iron and steel, TiC, niobium carbide (NbC), vanadium carbide (VC) and other substances are deposited to improve mechanical properties. Solidified transition metal atoms and carbon (C) atoms are deposited as a compound phase, so initially a "coherent interface" in which the iron atoms and carbon atoms meet in a coherent fashion is formed between iron (Fe) (100) // TiC (100) and Fe[100] // TiC[110].
Due to lattice misfit, a coherent interface at which the soft iron stretches slightly in the direction parallel to the interface is formed. The coherent interface itself is stable. As the deposits grow, however, the strain energy on the iron side increases, until overall it outweighs the benefit of the coherent interface formation. At this point, it is predicted to change to a "partially coherent interface" that has less strain even though coherence is sacrificed in the process (see Figure). It is necessary to be able to handle both coherent and partially coherent interfaces with first-principles calculations, and to properly estimate the strain energy in the area around deposits. As the number of atoms in the cell is large (several thousand to several tens of thousands), first-principles calculations for partially coherent interfaces can only be executed using the combination of the K computer and OpenMX. At present, we are making good progress in obtaining calculated results for stable atomic arrangements and energy in partially coherent interfaces. With regard to the stress near the interface, QMAS calculations have resulted in the discovery of a new type of stress resulting from the electron structure of the Fe atoms at the interface, and this will no doubt attract considerable attention in academic circles. In iron and steel, solidified hydrogen tends to invite brittle fracture. Capturing the hydrogen at the interface between the deposits and the iron is expected to make it possible to prevent this brittle fracture. We plan to pursue a detailed study of hydrogen capture by determining the structure of coherent and partially coherent interfaces. We also hope to conduct large-scale calculations for dislocations and grain boundaries using OpenMX. In the case of dislocations, attention has focused on the need to understand the interaction between dislocations and the solidified additive elements.
Benefits for society
The development of structural materials with outstanding strength, toughness and thermal resistance will enable highly efficient energy conversion in various types of generators and internal combustion engines, as well as reduced energy consumption through the construction of lightweight transport vehicles. This technology will also be indispensable for building highly reliable large structures and other elements of a safe and secure social infrastructure. Scarce elements are often used in the additive elements and alloy content of structural materials, and the understanding on a microscopic level that will be provided by research achievements in this area will make a major contribution to the technical development of substitutes for scarce elements.
|
|
| Model of compound / iron coherent interface (left) and partially coherent interface (right). Example of NbC (100) / Fe(100) interface. (Prepared by Hideaki Sawada of Nippon Steel & Sumitomo Metal Corporation). |