Development of variational Monte Carlo method and study of quantum spin liquid

Satoshi Morita	Graduate School of Engineering, The University of Tokyo

Strongly correlated electron systems show many interesting phenomena such as superconductivity and quantum spin liquid (QSL), and attract increasing attention not only as research subjects for fundamental physics but as next-generation devices. In order to simulate strongly correlated electron systems, we have developed the variational Monte Carlo method, which can treat large-size system with high accuracy.
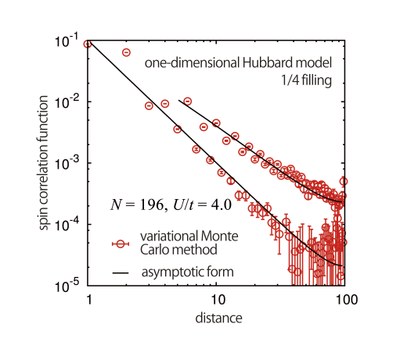
As a CMSI researcher, I have optimized the many-variable variational Monte Carlo method on the K computer and applied this method to study QSL. I finally achieve about 60 times speed-up and more than 90% parallelization efficiency in about 20,000 nodes. Such a speedup and high parallelization are making it possible to simulate a more complicated system in a realistic computational time. We also confirm that this method produces highly accurate results consistent with the exact theory in the one-dimensional Hubbard model.
Quantum spin liquid is a state in which spins fluctuate like a liquid. Competing interactions (geometrical frustration) and quantum fluctuations destroy magnetic order even at zero temperature. Since a QSL state is controllable with small external force, it has potential of application as a new magnetic device. The J₁-J₂ Heisenberg model on square lattice is one of the typical systems which are expected to realize QSL. We reveal that the generalized variational wave-function with the quantum number projection in the many-variable variational Monte Carlo method can represent a QSL state with triplet spin gap. A future challenge is to elucidate physics of QSL in ab initio effective models.

Spin correlation function of the one-dimensional Hubbard model. The numerical data are in excellent agreement with theoretical curves for Tomonaga-Luttinger liquid, which has large quantum fluctuations specific to one-dimensional systems.