From the Front Lines of Application Development 7 th Interview with Tomohiro Takaki, Developer of Phase-Field Method

Blurring the boundaries can sometimes produce better results. For example, if you go to Kyoto's famous Gion Festival, you can see European and Middle Eastern objects among the decorations on the festival floats. You realize that not adhering strictly to the boundaries between Japanese and Western elements has helped to perfect Kyoto's dazzling traditional culture. Even in the world of computational science that is strictly ruled by ones and zeros, there are methods in which computations are performed successfully by blurring the boundaries. In this issue, we focus on one such method, the Phase-Field (PF) method, and its developer Tomohiro Takaki, Associate Professor at Kyoto Institute of Technology.
Interviewee:
Tomohiro Takaki / Associate Professor, Graduate School of Science and Technology, Kyoto Institute of Technology
Interviewer:
Shingo Yonezawa / Assistant Professor, Graduate School of Science, Kyoto University
A Computational Techniquethat Blurs Boundaries
Our world is a world of many interfaces. When you put ice into a glass of water, the boundary between ice and water becomes an interface. If you magnify the interior of the metal around you, you can detect the presence of crystal grain bou daries and composition boundaries, and these interfaces hold the key to the nature of that material. Moreover, interfaces can change position and grow. In the former case, the interface will move if the ice melts or the water freezes. In the latter case, the interfaces in the metal material will be transformed by temperature and external pressure. Such interface behavior is extremely important to both science and engineering.
So how can interfacial changes be correctly simulated? A simple answer is to calculate the moment-by-moment changes in the location of the interface (Fig. 1(a)). However, the shape of interfaces frequently becomes complex. For example, it is well known that snow crystals have an extraordinarily complex structure. This is surely because the interface between ice and water vapor in clouds developed in a complex fashion. The more complex an interface is, the more difficult it is to perform calculations when the method of tracking the interface is employed. Particularly in the case of extremely detailed shapes, it becomes impossible to correctly calculate the energy originating from the curvature of the interface, and this can deal a fatal blow to the effort to accurately simulate the interface.
With such a conventional approach, the same mathematical formula can not be used to express both sides of the interface, so the range in which the mathematical formula can be used (= the interface) has to always be defined. To put it another way, various mathematical formulas and variables changes at the interface in a discontinuous manner, and this is a problem. If this is the case, we can approach the problem from a different perspective and try blurring the interface a bit (Fig. 1(b)). 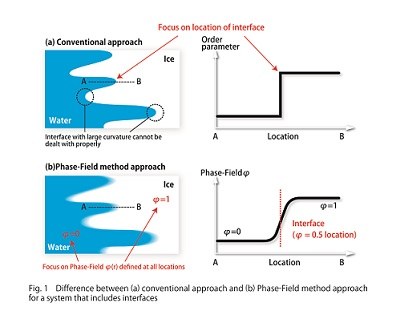 When we do that, the discontinuities are resolved and the mathematical formulas are connected to one another smoothly throughout the entire region that includes the interface. However, it in turn becomes impossible to properly determine the interface with this approach, so an additional variable φ is introduced. This variable is defined for the entire region and changes precipitously but smoothly in the neighborhood of the inte face. For example, φ is determined so that φ = 1 in ice and φ = 0 in water, and at the interface φ changes smoothly from 1 to 0. Moreover, the “real” int rface is set at the position where φ is equal to 0.5. As this variable φ is like a “field” that defines the phase on both sides of the interface, it is known as the Phase-Field (PF). Subsequently, by simultaneously computing equations that express the relationship between φ and various other quantities and equations that denote the time changes for these quantities, it is possible to calculate the changes in the interface. Moreover, the curvature energy in the interface is incorporated naturally into this model. In other words, one can accurately simulate interfaces with complex shapes, which are difficult to calculate with the conventional method. The method that introduces this PF to handle systems that include interfaces is known as the Phase-Field method (PF method).
When we do that, the discontinuities are resolved and the mathematical formulas are connected to one another smoothly throughout the entire region that includes the interface. However, it in turn becomes impossible to properly determine the interface with this approach, so an additional variable φ is introduced. This variable is defined for the entire region and changes precipitously but smoothly in the neighborhood of the inte face. For example, φ is determined so that φ = 1 in ice and φ = 0 in water, and at the interface φ changes smoothly from 1 to 0. Moreover, the “real” int rface is set at the position where φ is equal to 0.5. As this variable φ is like a “field” that defines the phase on both sides of the interface, it is known as the Phase-Field (PF). Subsequently, by simultaneously computing equations that express the relationship between φ and various other quantities and equations that denote the time changes for these quantities, it is possible to calculate the changes in the interface. Moreover, the curvature energy in the interface is incorporated naturally into this model. In other words, one can accurately simulate interfaces with complex shapes, which are difficult to calculate with the conventional method. The method that introduces this PF to handle systems that include interfaces is known as the Phase-Field method (PF method).
It was Ryo Kobayashi of Hiroshima University who demonstrated the utility of the PF method. Kobayashi is a very famous applied mathematician who, among other achievements, has received the Ig Nobel Prize twice for research into path determination by slime mold. He used the PF method to simulate the growth of dendrites in metal, successfully recreating their distinctive fractal-like structure. There is an anecdotal account that the research paper for this study was not released for a long time after the first demonstration, and Kobayashi finally published a paper on it several years later at the request of overseas researchers. Even so, it has become an extremely influential paper that has been cited more than 600 times.
Takaki's Encounter with the Phase-Field Method
Even before he encountered the PF method, Takaki had been pursuing research into experiments and simulations involving machine components. His primary simulation technique was the finite element method , in which the object is divided into tiny domains to perform computations. Beginning around 2000, however, finite element method software for general use gradually became available, and companies came to actively use this method as well. Under these circumstances, Takaki began to wonder whether it was appropriate to conduct research at a university that could be performed even by private sector companies. At around the same time, the PF method was included in a topic presented to him by his former instructor, Yoshihiro Tomita. The focus of Takaki's research at that time was the mechanical properties of macroscopic materials, and these are strongly controlled by ever finer microscopic crystalline structures. For example, to make a Japanese sword, the swordsmith heats and hammers steel to create a steel body that is far tougher than the original material, and the changes in the crystalline structure play a major role in this process. Takaki was attracted to the PF method, which can be used even for the formation of crystalline structures, and he sensed that it had great future potential, so he made it his research target.
Tomohiro Takaki
Associate Professor at Kyoto Institute of Technology. Currently conducting research in an effort to expand the use of the Phase-Field method in many other fields in addition to the machine field. Has received many awards for his work on the Phase-Field method, including the Gordon Bell Prize (Scalability / Time to Solution Prize) in 2011, the APACM Award for Young Investigators in Computational Mechanics, and the Certificate of Merit for Best Presentation, JSME Medal for Outstanding Paper and the Computational Mechanics Achievement Award of the Japan Society of Mechanical Engineers. |  |
|---|
Immediately after he began studying the PF method, Takaki was able to understand the trengths of the method. Firstly, one of the major characteristics of the PF method is its great compatibility with various other methods. For example, when combined with thermal diffusion equations, it can describe phenomena like coagulation that produce latent heat. When combined with fluid equations, it can describe the movement of interfaces with a presence of convection currents. As he had expected, Takaki also confirmed that the PF method has extremely high compatibility with the machine field. At academic societies that he belonged to in the machine field, initially there were only a few people who gave presentations on the PF method, but almost immediately the method was accepted and its use became more widespread. Takaki speaks humbly about that time. “In some ways, I was just in time to ride the wave.” But rather it can be said that he played a central role in creating that wave. Even after he moved to Kyoto Institute of Technology in 2007, Takaki pursued research centering on the PF method. Many researchers study the PF method as a means of applying it in their own field of research. In contrast, Takaki says that he wants to do anything and everything that can be done with a central focus on the PF method itself. In the sense of using the PF method as a point of departure for research, Takaki may be the only PF method specialist in Japan. At present, he is engaged in research in a wide range of fields - not only the growth of crystalline structures and changes in those structures, but also growth models for nerve cells, simulations of crack progression within materials, optimization of the structural configuration for supporting force and so on.
Even Greater Power with Supercomputers
One problem with the PF method is that of computation time. In order to describe complex interfacial structures, a fine mesh is needed for calculation, and this increases the quantity of calculations that must be performed. In particular, three-dimensional computations are needed for the simulations to be useful in the real world. But the number of meshes needed for three-dimensional calculations is several orders of magnitude greater than two-dimensional calculations, something that is beyond the capabilities of ordinary computers.
This is where supercomputers can demonstrate their true power. The great affinity between supercomputers and the PF method was demonstrated in various ways in 2011, when Takaki and coworkers received the Gordon Bell Prize, sometimes called the Nobel Prize of the supercomputing world. The prize was awarded for the work of a group including Takaki in the three-dimensional simulation of the dendrite growth of an alloy with an extremely fine mesh (several thousand × several thousand × several thousand), performed using the Tsubame 2.0 supercomputer at Tokyo Institute of Technology. Because the PF method requires a comparatively large number of computations for each mesh, it is a method that makes it easy for supercomputers to prove their worth. Many modifications were made to the memory access method and so on, resulting in the achievement of an extremely high execution performance of 2 petaflops. Takaki says that the receipt of the Gordon Bell Prize brought the PF method to the attention of many people outside the field. Future generations will undoubtedly see the award as one of the turning points for the PF method.
Another method in which supercomputers are expected to demonstrate their effectiveness is multi-scale computing. First, a macro scale test specimen is partitioned using the finite element method, and the deformation, internal stress and other attributes are calculated for each section. Normally that would be the end of it, but thanks to Takaki, it is now possible to use the PF method to calculate the changes in crystalline structure produced inside each element. As the mechanical properties of each element are changed as a result of these structural changes, the finite element method and PF method are performed again with these changes reflected. This process makes it possible to simulate macro-scale deformation while incorporating real-world phenomena on the micro level (for example, increased hardness of heavily-deformed sections). Such multi-scale computations take a very long time, so up to now only small domains could be handled. But if a supercomputer is used, multi-scale computation of real-world size materials will become possible.
The Future of the Phase-Field Method
How will the PF method develop from this point on? Takaki thinks that, as a first step, it will be important to conduct coagulation simulations that more accurately reflect the effect of convection currents. When a substance coagulates, convection currents must be produced on the liquid side, and therefore there should be many phenomena that cannot be reproduced unless these are accurately taken
into consideration. He also thinks that it will be necessary to build a methodology that links the PF method with first-principles calculations and other atomic scale computations. If these efforts bear fruit, it will become possible to simulate various processes in material manufacture, and this will produce innovations in material research. Secondly, Takaki thinks that steady efforts to compare
theory and experiments in greater detail will also be important.
Takaki is also working to expand the use of the PF method through a wide variety of activities. He has created a website (http://www.pfm.kit.ac.jp/) to collect issues relating to the PF method, and he has also published books aimed at beginners, held workshops and so on. On the other hand, the completion of a stand-alone application is still a work in progress. By itself, the PF method holds little interest; it becomes capable of performing meaningful simulations when it is combined with other equations. Because of this characteristic, it is likely to be difficult to develop a general PF method application that can be used for anything and everything. Takaki's first step will be to release it as a tool that can be incorporated into other programs, like a library, in order to enable as many people as possible to use the PF method.
In the meantime, the further innovations produced by Takaki and the PF method are coming soon to an interface near you.
◆Interviewer's Postscript
Shingo YonezawaThis interview was conducted on a hot summer day in August. But it was one surprise after another, with Prof. Takaki showing me several very interesting simulation results. I was particularly impressed with the multi-scale simulation. I was surprised at what can be accomplished with the Phase-Field method. To tell the truth, the basic equation used in the Phase-Field method takes almost the same form as the equation describing the superconducting state, which is my own research area. So I felt a real sense of affinity as I conducted this interview. |  |
|---|