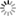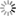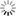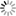From the Front Lines of Application Development Interview with Takeshi Nishimatsu, developer of feram
|
Interviewee :
|
 |
High hopes for FeRAM nonvolatile
memory
Have you ever heard the term “ferroelectrics?” If you apply an electric field to an insulator from the outside, the material itself develops a charge bias (becomes polarized). Materials that have this property are called dielectrics. Some of these materials exhibit polarization that is an order of magnitude larger than the others, and they are known as ferroelectrics. Not only ferroelectrics produce large polarization, but also the pontaneous polarization remains even if no external electric field is applied. Furthermore, if a reverse electric field is applied, the charge bias within the ferroelectrics is reversed. Materials that are known to be ferroelectrics include ceramics such as barium titanate and lead zirconate titanate (PZT). Barium titanate was dis covered in 1942 in the United States and at roughly the same time in former Soviet Union and Japan in 1944. Since that time, it has attracted a great deal of attention in the material field for its high electric permittivity, and considerable research has been conducted in an effort to develop practical applications.
In recent years, particular attention has focused on computer memory as an example of applications for FeRAM. As PCs become ever smaller and faster, they need new types of memory. The development of FeRAM (ferroelectric random access memory), made by combining layers of PZT and other ferroelectric thin films, is one example. As FeRAM uses ferroelectrics, it is possible to create memory from which information does not disappear when the power is turned off (nonvolatile memory). If a computer is equipped with FeRAM, application programs, which are used before shut down, can be restarted up as soon as the power is turned on, making computer operation faster, more convenient and more energy conservable. However, some problems must be resolved before FeRAM can be used as computer memory. Currently there are some examples of the practical application of FeRAM, such as in IC cards. However, the downsizing is not enough to enable FeRAM to be employed to create giga-bit memory chips for practical use as computer memory. For example, “dead layers” that resist polarization are produced between the electrode and the ferroelectric thin film, and these are said to affect capacitor performance, making material design difficult. But the thickness of the tiny thin film measures only several tens of nm, so it is difficult to observe directly and hard to determine exactly what phenomenon is occurring. For this reason, the use of computer simulations is expected to play a major role in research in this area.
Calculating dipole behavior
feram, the application program developed by Dr. Nishimatsu, is a molecular dynamics program capable of realistically simulating thin film sizes on the order of several tens of nm. feram is available worldwide as free software, and people are free to use, modify and redistribute the program. Currently, if I google the word “feram”, its homepage ranks in top 10. The software package has been downloaded more than 900 times. “I’ve also benefitted from free software, so I released feram so that anyone can easily reproduce simulations to check the results of my research,” says Dr. Nishimatsu. “I named it feram, like FeRAM, to make it easy for people to find on the Internet. I’d like both memory developers and researchers to use feram.” How does feram simulate ferroelectric thin films? It is easiest to explain using the concept of the dipole. Electrons, which have a negative charge, cannot move freely within dielectrics. In that case, how is it possible for such substances to have an electric bias? If a dielectric substance is placed under an electric field, the positions of the atoms in the crystal are displaced slightly, producing an electric bias within a tiny area. This can be thought of as the positive and negative point charges being separated by a tiny distance. This state is called an electric dipole (or simply dipole). The movement of these dipoles determines the electric bias of the substance as a whole. In the first stage of ferroelectric thin film simulation, the properties of the ferroelectrics are determined by means of first principles calculations. In the case of barium titanate, the subject of calculations is a unit lattice cube, with each side measuring 0.4 nm and made up of one titanium atom, one barium atom and three oxygen atoms. First-principles calculations can be used to determine the lattice constant, elastic constant and lattice vibration (phonon properties) comparatively easily and with a high degree of precision. Next, the relationship between the energy and the degree of displacement of the atoms is investigated. The distinguishing characteristic of ferroelectrics is that spontaneous polarization occurs, meaning that the atoms are displaced. When the atoms in the unit lattice are displaced, the energy in the lattice overall changes. Dr. Nishimatsu modified the free software first-principles program ABINIT to develop a program that can determine various parameters in such a way that energy is at a minimum with respect to the displacement of atoms. These parameters are constructed as effective Hamiltonians required for molecular dynamics calculations in feram. “25 parameters are determined in first-principles calculations,” says Dr. Nishimatsu. “It’s difficult to determine so many, so I modified ABINIT to make it easy to have them calculated automatically.” Dr. Nishimatsu says this is one area of research in which he has poured his heart and soul. Using the 25 parameters determined with first-principles calculations, molecular dynamics calculations are performed using feram. With feram, the key is how to express the interaction between dipoles. Dipoles exert force on each other in inverse proportion to the cube of the distance between them. The dipoles are placed in each unit cell of a lattice called a supercell, a cube with each side consisting of several tens of cells, and the force acting between the dipoles is calculated in order to simulate the movement of dipoles over time. The distinguishing characteristic of feram is that conditions such as temperature and external electric fields that are difficult to incorporate into first-principles calculations can be
varied in the simulation.
 |
Takeshi Nishimatsu
|
feram makes fast Fourier transform possible
Dr. Nishimatsu says that the nature of the force acting between dipoles is anisotropic long-range force. As the effect is greater in dipoles that are farther away from one another, tiny changes in form on the part of the objects being simulated change the movement of the dipole as a whole. A particularly important issue is how to treat the edges of the objects. Even if, from a broad perspective, the boundary between the object and the other space appears to be clearly visible, from the narrow perspective, electrons exhibit complex behavior near this boundary. As the boundary between the object and the surrounding space cannot be clearly determined, it is difficult to simulate. This problem of the boundary is itself an intriguing topic for research, but it becomes a troublesome problem when, as in the case of the present objective, we want to know the behavior of fairly large systems. Moreover, because the interaction between dipoles is long-range force, the fact that the results of calculation will be different for infinite systems and (finite) systems that have edges is also a problem. Finiteness of the systems also poses disadvantages in terms of calculation methods. It would take an extremely large amount of time to calculate the long-range force between dipoles on a realistic scale. Even for a thickness of some tens of nm, when converted into dipole layers, this becomes large-scale calculations for more than 100 layers.
“The edge problem and the problem of calculation speed were headaches. But one day, in the course of discussions with Prof. Waghmare, I hit upon an outstanding idea that could solve them both,” says Dr. Nishimatsu, speaking excitedly. What was this idea? The structure of a thin film capacitor is that of a thin film of ferroelectrics placed between two metal plates. If the ferroelectric thin film becomes spontaneously polarized, an electric charge appears on the surface of the thin film. If the two metal plates are connected with an electric wire, the electrons in the metal can move freely, so a charge that is the opposite of that in the thin film will appear on the surface of the metal plates. It is as if the ferroelectric thin film is sandwiched between two mirrors: the two metal plates function as opposite mirrors, and infinite images of the ferroelectrics appear beyond the opposite mir for research, but it becomes a troublesome problem when, as in the case of the present objective, we want to know the behavior of fairly large systems. Moreover, because the interaction between dipoles is long-range force, the fact that the results of calculation will be different
for infinite systems and (finite) systems that have edges is also a problem. Finiteness of the systems also poses disadvantages in terms of calculation methods. It would take an extremely large amount of time to calculate the long-range force between dipoles on a realistic scale. Even for a thickness of some tens of nm, when converted into dipole layers, this becomes large-scale calculations for more than 100 layers.
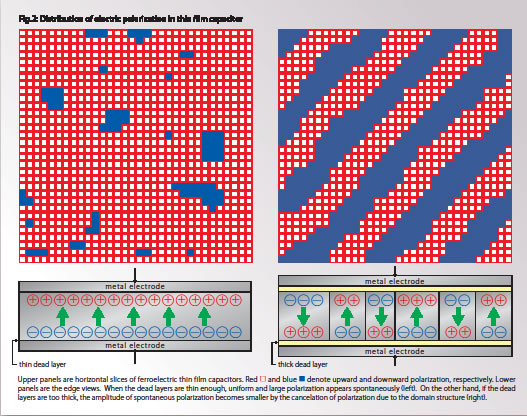
“The edge problem and the problem of calculation speed were headaches. But one day, in the course of discussions with Prof. Waghmare, I hit upon an outstanding idea that could solve them both,” says Dr. Nishimatsu, speaking excitedly. What was this idea? The structure of a thin film capacitor is that of a thin film of ferroelectrics placed between two metal plates. If the ferroelectric thin film becomes spontaneously polarized, an electric charge appears on the surface of the thin film. If the two metal plates are connected with an electric wire, the electrons in the metal can move freely, so a charge that is the opposite of that in the thin film will appear on the surface of the metal plates. It is as if the ferroelectric thin film is sandwiched between two mirrors: the two metal plates function as opposite mirrors, and infinite images of the erroelectrics appear beyond the opposite mirrors (Fig.1). In other words, the thin film is the only area being calculated, but an infinite series of mirror images are displayed above and below the thin film. “When I came up with the idea for the opposite mirror, I thought, Eureka!” says Dr. Nishimatsu. “Using feram to perform calculations considering the thin film as an infinite, periodic structure makes it possible to use fast Fourier transform. And, as a result, much faster calculations can be achieved than was possible up to now. Only my feram program uses fast Fourier transform to perform simulations of ferroelectric thin film capacitors.” Already, Dr. Nishimatsu’s research has clarified the adverse impact of dead layers (Fig.2) on the performance of ferroelectric capacitors and the manner in which these adverse effects are manifested, by calculating hysteresis loops ̶ which indicate how the charge bias of thin films will change in response to changes in electric fields applied externally ̶ when dead layers are present. In the future, Dr. Nishimatsu wants to study new ways to expand the potential of supercomputers. Modylas and RSDFT, which have been introduced previously in this series, improved internodal communication to achieve large-scale computing using as many nodes as possible. In contrast, feram uses only a single node. “In material development, it’ s important to draw a phase diagram,” says Dr. Nishimatsu. “The large capacity of a supercomputer (capacity computing) can be used to determine how properties change as a result of changes in temperature and external electric fields. By varying the conditions and performing numerous calculations for a single node, you can accumulate the statistical data needed to draw a phase diagram. I want to use feram to develop new uses for supercomputers.” feram seems poised to discover new and expanded potential for supercomputers.
 |
Yoshimi Kubota
|
 |