Markov Chain Monte Carlo Method without Detailed Balance
 The emergences of phase transition and strongly correlated states, in which we are very interested, include an abundance of novel physics, and they are expected to have many applications in new material design and so on. The essence of these physical phenomena is that they are
The emergences of phase transition and strongly correlated states, in which we are very interested, include an abundance of novel physics, and they are expected to have many applications in new material design and so on. The essence of these physical phenomena is that they are
multi-particle (have multiple degrees of freedom), and it is not effective to conduct rough approximation that considers only average quantities among particles. Only through the skillful use of computers is it possible to analyze these problems that are difficult to solve using manual calculation by human beings.
However, these problems cannot be solved using a shotgun approach with computers on a large scale; the key is how cleverly and efficiently they can be used. This also applies to the Markov chain Monte Carlo method with which we are working. This method, in which multiple integrations are derived using a computer, has great general applicability, and it is becoming indispensable not only in physics but also in various other fields, such as, chemistry, biology, medicine, statistics and economics. Almost all of the Markov chain Monte Carlo methods up to now used a condition of " detailed balance," and for more than half a century the method continued to develop within the boundaries of this condition. However, the detailed balance was used because of the convenience for computation; it was not a fundamentally necessary condition. Accordingly, we broke with what had been up to now established and devised a new algorithm that can calculate correctly even without satisfying the detailed balance. This algorithm uses a geometrical process called as "weight filling" that definitely minimizes the average rejection rate, which is the cause of reduced efficiency, making it even zero in most cases (see figure). This greatly improved calculation efficiency to anywhere from several times to more than a hundred times as much as that by conventional methods. Applying the algorithm to spin systems, which are quantum-mechanical problems, resulted in the discovery of a new phase transition for spins from a liquid state to a solid state. This method is applicable to almost all of the Markov chain Monte Carlo methods that are used in various fields, and it is expected to make wide-ranging contributions in the future.
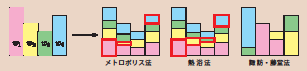
Comparison of the "weight filling" process using the new method and existing methods. In this case, the rejection rate is reduced to zero by our method.